Motivation

In the Disney BSDF lecture I met the idea of a complex index of refraction. Disney only uses Schlick’s approximation, but that glimpse made me curious: what is a complex \(η\) and where does it come from physically? Mid-quarter I was fascinated by wave-optics phenomena such as thin-film iridescence. Belcour’s paper looked daunting on first pass, yet the final project was a perfect excuse to dive in.

Key references I leaned on repeatedly:

The post follows the route I wish I’d had: physics → rendering theory → implementation.

Physical Model for Thin-Film Interference

This was the most fun (and the deepest rabbit-hole) — yet nothing beats seeing an equation-heavy model reproduce the hues of real steel.

Light as a Wave

Classical ray tracing treats light as straight-line rays — fine when obstacles are large relative to wavelength, but it misses interference. Light is in fact an electromagnetic wave; Fig. 1 shows orthogonal \(𝐄\) and \(𝐁\) fields.

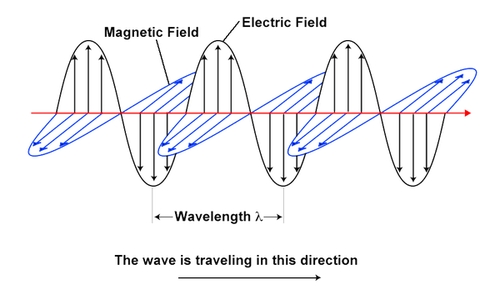
Figure 1 — Light as an electromagnetic wave

Figure 2 — Un-polarized light

Reflection/refraction are simply one wave meeting a medium boundary, its behaviour governed by Maxwell’s equations

\[\nabla\!\cdot\mathbf E = \frac{\rho}{\varepsilon_0}, \quad \nabla\!\cdot\mathbf B = 0, \quad \nabla\times\mathbf E = -\frac{\partial\mathbf B}{\partial t}, \quad \nabla\times\mathbf B = \mu_0\mathbf J + \mu_0\varepsilon_0\frac{\partial\mathbf E}{\partial t}.\]

From them we derive the plane-wave solution

\[\mathbf E(z,t) = E_0\,\hat{\mathbf x}\cos(kz-\omega t),\qquad \mathbf B(z,t) = B_0\,\hat{\mathbf y}\cos(kz-\omega t),\]

or, compactly,

\[\mathbf E(\mathbf r,t)=\Re\{\mathbf E_0\,e^{i(\mathbf k\!\cdot\!\mathbf r-\omega t)}\}.\]

That complex form foreshadows the complex reflection coefficient.

Reflection & Refraction

At a boundary the tangential \(𝐄\) and \(𝐇\) components must satisfy continuity conditions (from the integral Maxwell form).
Wave-front matching yields Snell’s law

\[η_1\sin\theta_1 = η_2\sin\theta_2 .\]

To obtain amplitudes we return to those boundary conditions, and derive the Fresnel amplitude coefficients

\[r_\perp = \frac{\cos\theta_i - η\cos\theta_t}{\cos\theta_i + η\cos\theta_t},\qquad r_\parallel = \frac{-η\cos\theta_i + \cos\theta_t}{η\cos\theta_i + \cos\theta_t},\]

with \(η = η_2/η_1\) (and analogous \(t_\perp\), \(t_\parallel\)).
Power, not amplitude, matters for radiance:

\[R = |r|^{2},\qquad T = \frac{η\cos\theta_t}{\cos\theta_i}|t|^{2},\qquad R+T=1.\]

Complex Index of Refraction

For conductors the material conductivity \(σ\) gives

\[η = \sqrt{\Bigl(\varepsilon' + i\,\frac{σ}{\omega\varepsilon_0}\Bigr)\mu_r}\;=\;η_R+iη_I ,\]

so \(η\) is complex; the imaginary part models absorption (skin-depth attenuation).

Thin-Film Interference

A thin film adds a second interface (Fig. 3).
Two closely spaced reflected rays acquire a phase difference

\[\Delta\phi = \frac{2\pi\mathcal D}{\lambda},\qquad \mathcal D = η_2(AB+BC) - η_1 AD,\]

creating interference.
Summing all paths (the Airy summation)

\[r = r_{12} + \sum_{k=1}^{\infty} t_{12} r_{23}(r_{21}r_{23})^{k-1} t_{21} e^{ik\Delta\phi}\]

yields the closed-form

\[r = r_{12} + \frac{t_{12} r_{23} t_{21}\,e^{i\Delta\phi}}{1 - r_{21} r_{23}\,e^{i\Delta\phi}} ,\]

and, for un-polarized light,

\[R = \tfrac12\!\left(|r_\perp|^{2} + |r_\parallel|^{2}\right).\]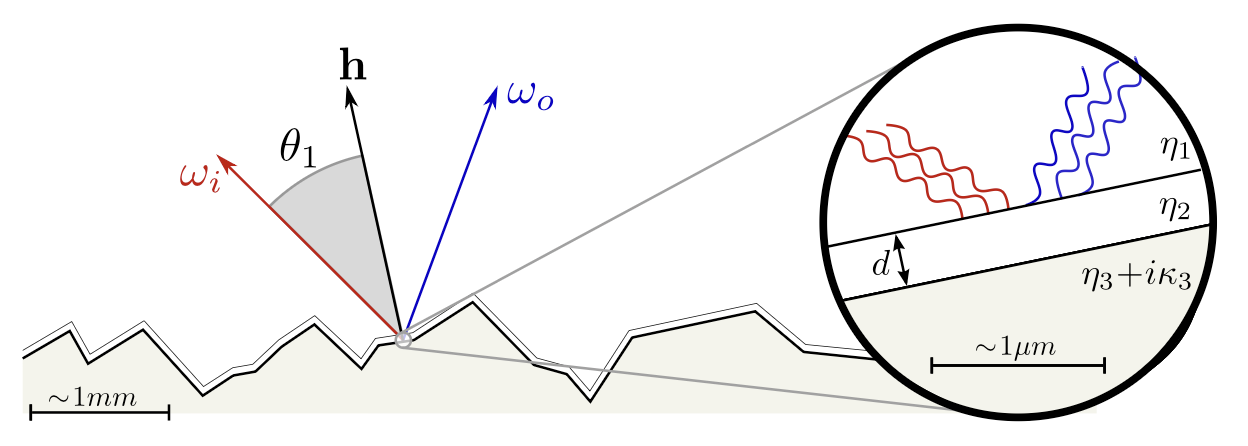

Figure 3 — Thin-film geometry

Rendering

BRDF Model

Belcour replaces the Schlick Fresnel term in the micro-facet BRDF with Airy reflectance \(R\):

\[\rho(\omega_o,\omega_i;\lambda)= \frac{D(\mathbf h)\,G(\omega_o,\omega_i)\,R(\mathbf h\!\cdot\!\omega_i;\lambda)} {4(\omega_o\!\cdot\!\mathbf n)\,(\omega_i\!\cdot\!\mathbf n)}.\]

Because \(R\) depends on wavelength \(\lambda\), an RGB renderer must spectrally integrate it.

Spectral Integration

Human cones integrate spectrum into three LMS values, converted to RGB.
Analogously we pre-integrate BRDF & lights per band:

\[\rho_j(\omega_o,\omega_i)= \int \rho(\omega_o,\omega_i;\lambda)\, \frac{s_j(\lambda)}{\|s_j\|}\,d\lambda ,\]

so only the reflectance term needs integration:

\[R_j(\mathbf h\!\cdot\!\omega_i)= \int R(\mathbf h\!\cdot\!\omega_i;\lambda)\, \frac{s_j(\lambda)}{\|s_j\|}\,d\lambda .\]

Belcour’s Fourier Solution

Re-writing the Airy series as

\[R = C_0 + 2\sum_{m=1}^{\infty}C_m\cos(m\Phi),\]

and assuming Fresnel amplitude/phase constant per band, a change of variable to frequency \(\nu\) plus Parseval gives the analytical band-integrated result

\[\boxed{ R_j = C_0 + 2\sum_{m=1}^{\infty}C_m \begin{bmatrix}\cos(m\phi_2)\\\sin(m\phi_2)\end{bmatrix}^{\!\!T} \begin{bmatrix}\Re_j(m\mathcal D)\\\Im_j(m\mathcal D)\end{bmatrix}}.\]

\(\Re_j,\Im_j\) are the real/imaginary parts of the Fourier-transformed sensor curves, tabulated or Gaussian-fitted.

Implementation

I added a new material in La Jolla Renderer:

struct IridescentRoughConductor {
    Texture<Real> roughness;
    Texture<Real> anisotropic;
    Texture<Spectrum> film_texture;

    // Conductor base
    Real eta;   // real part
    Real k;     // extinction coeff.

    // Thin-film layer
    Real film_eta;
    Real min_thickness;   // nm
    Real max_thickness;   // nm
};

Replaced the Cook–Torrance Fresnel with the analytic \(R_j\) above (using \(m\in[1,3]\)).
Transmittance is \(T=1-R\) per energy conservation.
Gaussian fits and look-up tables were ported from the authors’ Mitsuba plugin.

Scene & Results

Reference photos of differentially tempered steel:

Rendered in La Jolla (large dome light above, iron base \(η=2.7, κ=2.8\), oxide film \(η=2.9\), thickness 10–70 nm):

Parameter sweeps (film \(η=1.33\)):

Conclusion

Belcour’s thin-film BRDF slots neatly into a micro-facet framework once an analytical band integration is available. The Fourier-domain trick keeps evaluation fast enough for interactive tweaking, and the rendered steel convincingly reproduces real iridescent hues.

Future work: importance-sample the interference term for fewer Monte-Carlo samples, and extend to spatially varying film thickness maps captured from real objects.